2 Classical Test Theory
In Psychology, questionnaires or scales are a crucial part of the assessment. These scales provide importante information about a person. For instance, when doing an educational assessment, a test score on the exam can be a key indicator of the extent to which the person has mastered the knowledge of that domain.
In psychometric latent variable modeling, measurement occurs when a test score reflects a persons’ ability in a specific area. However, this score is far from reflecting this ability in a perfect manner. It’s easy to see that a person can vary its performance in an educational test if they answer in different times, Thus, the examination is not perfect, and has what we call measurement error. In addition, the ability is an unobserved variable (i.e., not observed directly, but inferred by a persons’ score). To take all of this into account, a classical test theory (CTT) have been proposed to evaluate scale scores.
2.1 Overview of Classical Test Theory
In CTT, the main idea is that the score of a participant in a given assessment (denoted as \(X\)) can be decomposed into their true score (\(T\)) and a random error component (\(E\)): \[ X = T + E \] \(T\) can be defined as the expected value of the observed score over an infinite number of repeat administrations in the same examination. Or, \(T\) can be thought as the score if the scale was perfectly measuring the ability of a given person (i.e., without the measurement error). \(X\) is the raw score of the participant, and \(E\) is the measurement error. Figure 2.1 shows the relationship between these elements.
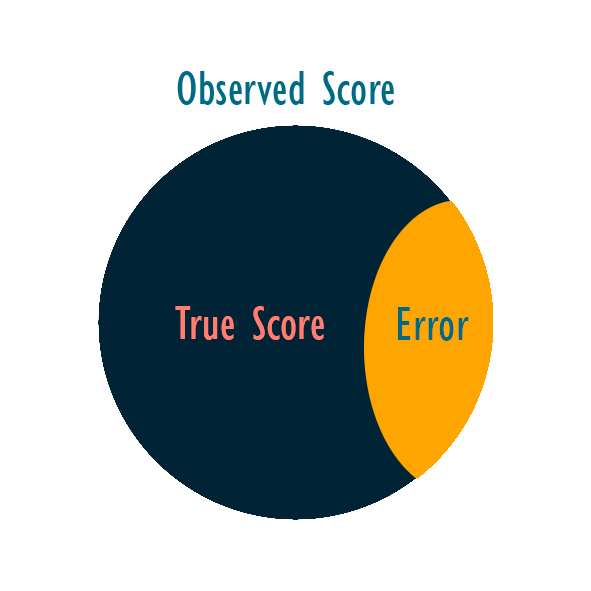
The main task for CTT is to elaborate strategies to control or evaluate the magnitude of \(E\). While \(E\) can be caused by a number of factors, such as problems with the test, bias from the participants, historical or environmental factors, etc. (Pasquali, 2017). However, there’s no way to know the true score (\(T\)) of a participant if there were no measurement error (\(E\)). In fact, both \(T\) and \(E\) are unobserved variables. Thus, to use this model, we have to make our first assumption: one can define \(T\) as the expected value of the observed scores X (i.e., \(E(X)=T\)), which leads to the expected value of E being zero (\(E(E)=0\)); or one can define the expected value of \(E\) as zero, which leads to \(T\) being the expected value of \(X\). Both ways of proceeding with the assumption lead to the same result, but they differ with respect to what is assumed, and what is a consequence of the assumptions (Brennan, 2011).
The structure of the CTT model equation (\(X=T+E\)) bears a striking resemblance to a straightforward linear regression equation, leading one to interpret \(E\) merely as model fitting error in the conventional statistical sense. However, such an interpretation is, at best, misleading. The CTT model operates as a tautology, wherein all variables on the right-hand side remain unobservable, and these unobservable variables lack inherent meaning beyond the assumptions we impose on them. Notably, \(T\) does not possess an independent status from the other variables in the model, rendering it inappropriate to characterize \(E\) as a residual or model fitting error (Brennan, 2011).
2.2 Reliability in CTT
The standard definition of reliability typically refers to the squared correlation between observed and true scores, denoted as \(\rho^2(X,T)\). Additional expressions for reliability are provided below (Brennan, 2011):
\[ \rho^2(X,T)=\rho(X,X')=\frac{\sigma^2(T)}{\sigma^2(X)}=\frac{\sigma^2(T)}{\sigma^2(T)+\sigma^2(E)} \]
The last three formulations are typically obtained by assuming that, for an indefinitely large population of participants: (1) test forms (denoted as \(X\) and \(X'\)) are parallel, meaning they share identical observed score means, variances, and covariances, and they exhibit equal covariance with any other measure; (2) the covariance between errors for parallel forms is zero; and (3) the covariance between true and error scores is zero (Brennan, 2011). The reliability estimates tend to align more with the last two expressions in the equation provided earlier, both explicitly addressing true score variance, a value that remains elusive. Typically, these estimates leverage the understanding that the covariance between scores for classically parallel forms equals the true score variance, denoted as \(\sigma(X, X') = \sigma^2(T)\). Coefficient \(\alpha\) stands out as the most used among these coefficients.
2.3 References
Brennan, R. L. (2010). Generalizability theory and classical test theory. Applied measurement in education, 24(1), 1-21. https://doi.org/10.1080/08957347.2011.532417
Pasquali, L. (2017). Psicometria: teoria dos testes na psicologia e na educação. Editora Vozes Limitada.
